In this blog we will discuss the computation of dense sub-graph (community) of sparse graph, which is very common in our real life complex network. We will give introduction about different way of computing sub-graph and finally will spread some light on random walk approach.
Complex network has become important in
different domain such as sociology (acquaintance or collaboration networks),
biology (metabolic networks, gene networks) or computer science (Internet
topology, Web graph, P2P networks). The Graphs of these networks are general
globally sparse but locally dense. There exist group of vertices which are
highly connected among itself, called communities, but few links to other. This
type of structure carries much information about network. One real life example
could be our Facebook friends if we draw our friends as node and link between
them if they are friend among themselves then we will find a sparse graph
having different dense sub graph(community) based on college friend , High
school friend , School friend, colleague etc.
Community Computation problem can be
related to graph partition problem [1]in which given a graph G = (V,E) with V vertices and E edges,
k-way partition of graph is partitioning of graph in k part such that number of
edges running over these partitions are minimum. However the algorithm for
Graph partition is not well suited for our case, because no of communities and
their size is input for Community Computation.
Hierarchical clustering is another
classical approach in which nodes are grouped together based on the similarity
between nodes, Newman proposed [2] a greedy algorithm that starts with n
communities corresponding to the vertices and merges communities in order to
optimize a function called modularity which measures the quality of a
partition.
The approach which is discussed here is
based on the random walks on a graph [3] tend to get “trapped” into densely
connected parts corresponding to communities. The graph G has its adjacency
matrix A: Aij = 1 if vertex i
and j are connected and Aij =
0 otherwise. The degree d(i) of
the vertex i is the number of its neighbors. A discrete random walk is a
process in which a walker is on a vertex and moves to vertex chosen randomly
and uniformly among its neighbors. The sequence of visited vertices is a Mrakov chain, the states of which are
the vertices of the graph. At each step, the transition probability from vertex
i to vertex j is Pij =Aij/d(i).
This defines the transition matrix P of random walk. The probability of going
from i to j through a random walk of length t is (Pt)ij. It
satisfies following two properties of random walk.
Property 1: When length of a path between two vertices i and j tends toward infinity. The probability that a random walker will be at
vertex j will totally depend on the degree of vertex j
Property 2: The ratio of
probabilities of going from i to j and j to i through a random walk of a fixed
length t depend on the degrees d(i) and d(j).
For grouping
vertices into communities, we will now introduce a distance r between the
vertices that captures the community structure of the graph. This distance will
be large if two vertices are in different communities, and on contrary if the
distance is small they will be in same community. It will be computed from the
information given by the random walk of the graph.
Let us consider a random walk of length t
from vertex i to j . t is large enough to gather the topology of graph.
However t must not be too long to avoid property
1. The probability Ptij would depend on the degree of the vertices i
and j. Each Ptij gives some information about the two
vertices i and j, but property 2 says
that Ptij and Ptji encode the same
information. Finally the information about vertex i is encode inside n
probabilities Ptik
1<k<n. Which is nothing but the ith row of matrix Pt.
For comparing two vertices we must notice following points.
·
If
two vertices i and j are in the same community, the probability Ptij
will be high be high but if Ptij
is high it does not necessarily imply that i and j will be in same community.
·
High degree vertex will have always high
probability that a random walker will reach there. So Ptij is influenced by the degree d(j) of
vetex.
·
Two
vertices of a same community observe all the other vertices in same way. Thus
if i and j are in same community
then
References
[1]Graph
Partition Problem
[2]Newman,
M.E.J.: Fast algorithm for detecting community structure in networks. Physical
Review E 69 (2004) 066133
[3]Computing
Communities in Large Networks Using Random Walks - Pascal Pons and
Matthieu Latapy








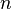
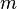
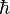

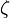



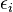 to each node, determined by its fitness through the relation
to each node, determined by its fitness through the relation
 . In particular when
. In particular when  all the nodes have equal fitness, when instead
all the nodes have equal fitness, when instead  nodes with different "energy" have very different fitness. We assume that the network evolves through a modified
nodes with different "energy" have very different fitness. We assume that the network evolves through a modified 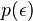 enters in the network and attach a new link to a node j chosen with probability:
enters in the network and attach a new link to a node j chosen with probability:
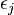
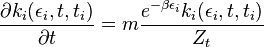
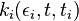 indicating the number of links attached to node i that was added to the network at the time step
indicating the number of links attached to node i that was added to the network at the time step  .
. 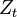 is the partition function, defined as:
is the partition function, defined as:

 satisfies
satisfies  ,
,  plays the role of the chemical potential, satisfying the equation
plays the role of the chemical potential, satisfying the equation
 and "fitness"
and "fitness" 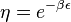 . In the
. In the  limit the occupation number, giving the number of links linked to nodes with "energy"
limit the occupation number, giving the number of links linked to nodes with "energy"  .
.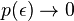 for
for 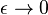 at high enough value of
at high enough value of 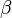 we have a condensation phase transition in the network model. When this occurs, one node, the one with higher fitness acquires a finite fraction of all the links. The Bose–Einstein condensation in complex networks is therefore a topological phase transition after which the network has a star-like dominant structure.
we have a condensation phase transition in the network model. When this occurs, one node, the one with higher fitness acquires a finite fraction of all the links. The Bose–Einstein condensation in complex networks is therefore a topological phase transition after which the network has a star-like dominant structure. , when the fittest node acquires a finite fraction of the edges and maintains this share of edges over time.
, when the fittest node acquires a finite fraction of the edges and maintains this share of edges over time.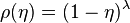
 of the system. In the end, the
of the system. In the end, the