Following up Dastagiri’s excellent post is a tough task. But, I will try my best, not to bore you with monotony of Dravid like defense after this type of Sehwagian start. After willfully taking up the challenge to contribute in this blogathon, I juggled with different types of random topics. Finally, I chose this topic which I feel, will perfectly set the premise to dive into the perplexities of complex networks.

The Large Hadron Collider

Most of the previous year was a dream-come-true times for any quantum physicist. The search of so-called God particle in the Haddron Collider caught the attention of all kinds of minds - be it Calvin or Mr. Bin. The quarrel among the quarks suddenly became the queen of most of the daily discussions. And all this hoopla of scientific gigantic leap was approximately based upon Bose-Einstein statistical model of particle physics. To be precise, the modelling of Bose-Einstein condensate (BEC) gave initial light upon the deepest of secrets of nature. Meanwhile, folks, lets gear up for a bit of physics to get a clear idea about BEC.

Bose–Einstein condensate:

Bose–Einstein condensate is a state of matter that occurs in certain gases at very low temperatures. Any elementary particle, atom, or molecule, can be classified as one of two types: a boson or a fermion. For example, an electron is a fermion, while a photon or a helium atom is a boson.

In quantum mechanics, the energy of a (bound) particle is limited to a set of discrete values, called energy levels. An important characteristic of a fermion is that it obeys the Pauli exclusion principle, which states that no two fermions may occupy the same energy level. Bosons, on the other hand, do not obey the exclusion principle, and any number can exist in the same energy level. As a result, at very low energies (or temperatures), a great majority of the bosons in a Bose gas can be crowded into the lowest energy state, creating a Bose–Einstein condensate.

So, a Bose–Einstein condensate is a state of matter of a dilute gas of bosons cooled to temperatures very near absolute zero (0 K or−273.15 °C). Under such conditions, a large fraction of the bosons occupy the lowest quantum state, at which point quantum effects become apparent on a macroscopic scale. These effects are called macroscopic quantum phenomena.

For all mathematical freaks,the transition to BEC occurs below a critical temperature, which for a uniform three-dimensional gas consisting of non-interacting particles with no apparent internal degrees of freedom is given by:

where:

$\,T_c$	is	the critical temperature,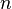
$\,n$	is	the particle density,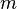
$\,m$	is	the mass per boson,
$\hbar$	is	the reduced Planck constant,
$\,k_B$	is	the Boltzmann constant, and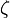
$\,\zeta$	is	the Riemann zeta function; $\,\zeta(3/2)\approx 2.6124.$

Briefly this is the sneak peek of this extremely complicated quantum phenomenon, and now look at the complex networking side of it.

Bose–Einstein condensation at 400, 200, and 50 nano-kelvins. The peaks show that as the temperature
goes down, more and more atoms "condense" to the same energy level.

Connection with network theory

Despite the irreversible and non equilibrium nature of complex networking systems, these follow Bose statistics and can undergo Bose–Einstein condensation. Addressing the dynamical properties of these non-equilibrium systems within the framework of equilibrium quantum gases predicts that the “first-mover-advantage,” “fit-get-rich,” and “winner-takes-all” phenomena observed in competitive systems are thermodynamically distinct phases of the underlying evolving networks.

Schematic illustration of the mapping between the network model and the Bose gas.

Starting from the fitness model, the mapping of a Bose gas to a network can be done by assigning an energy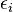 $\epsilon_i$ to each node, determined by its fitness through the relation

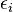$\epsilon_i=-\frac{1}{\beta}\ln{\eta_i}$

where $\beta=1\!$ . In particular when $\beta=0\!$ all the nodes have equal fitness, when instead $\beta\gg 1\!$ nodes with different "energy" have very different fitness. We assume that the network evolves through a modified preferential attachment mechanism. At each time a new node i with energy $\epsilon_i$ drawn from a probability distribution 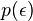$p(\epsilon)$ enters in the network and attach a new link to a node j chosen with probability:

$\Pi_j=\frac{e^{-\beta\epsilon_j}k_j}{\sum_r e^{-\beta\epsilon_r}k_r}.$

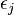In the mapping to a Bose gas, we assign to every new link linked by preferential attachment to node j a particle in the energy state $\epsilon_j$

The continuum theory predicts that the rate at which links accumulate on node i with "energy " 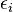$\epsilon_i$ is given by

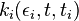$\frac{\partial k_i(\epsilon_i,t,t_i)}{\partial t}=m\frac{e^{-\beta\epsilon_i}k_i(\epsilon_i,t,t_i)}{Z_t}$

where $k_i(\epsilon_i,t, t_i)$ indicating the number of links attached to node i that was added to the network at the time step 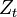$t_i$ . $Z_t\!$ is the partition function, defined as:

$Z_t=\sum_i e^{-\beta\epsilon_i}k_i(\epsilon_i,t,t_i).$

The solution of this differential equation is:

$k_i(\epsilon_i,t,t_i)=m\left(\frac{t}{t_i}\right)^{f(\epsilon_i)}$

where the dynamic exponent $f(\epsilon)$ satisfies $f(\epsilon)=e^{-\beta(\epsilon-\mu)}$ , $\mu$ plays the role of the chemical potential, satisfying the equation

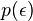$\int d\epsilon \, p(\epsilon) \frac{1}{e^{\beta(\epsilon-\mu)}-1}=1$

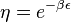where $p(\epsilon)$ is the probability that a node has "energy" $\epsilon$ and "fitness" $\eta=e^{-\beta \epsilon}$ . In the $t \rightarrow \infty$ limit the occupation number, giving the number of links linked to nodes with "energy" $\epsilon$ , follows the familiar Bose statistics

$n(\epsilon)=\frac{1}{e^{\beta(\epsilon -\mu)}-1}.$ .

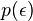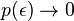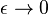The definition of the constant $\mu$ in the network models is surprisingly similar to the definition of the chemical potential in a Bose gas. In particular for probabilities $p(\epsilon)$ such that $p(\epsilon) \rightarrow 0$ for $\epsilon \rightarrow 0$ at high enough value of $\beta$ we have a condensation phase transition in the network model. When this occurs, one node, the one with higher fitness acquires a finite fraction of all the links. The Bose–Einstein condensation in complex networks is therefore a topological phase transition after which the network has a star-like dominant structure.

Bose–Einstein phase transition in complex networks

The mapping of a Bose gas predicts the existence of two distinct phases as a function of the energy distribution. In the fit-get-rich phase, describing the case of uniform fitness, the fitter nodes acquire edges at a higher rate than older but less fit nodes. In the end the fittest node will have the most edges, but the richest node is not the absolute winner, since its share of the edges (i.e. the ratio of its edges to the total number of edges in the system) reduces to zero in the limit of large system sizes . The unexpected outcome of this mapping is the possibility of Bose–Einstein condensation for $T<T_{BE}$ , when the fittest node acquires a finite fraction of the edges and maintains this share of edges over time.

A representative fitness distribution ρ(η) that leads to a condensations

$\rho(\eta)=(1-\eta)^{\lambda}\$

with λ = 1.

However, the existence of the Bose–Einstein condensation or the fit-get-rich phase does not depend on the temperature or $\beta$ of the system but depends only on the functional form of the fitness distribution $\rho(\nu)$ of the system. In the end, the $\beta$ falls out of all topologically important quantities. In fact it can be shown that Bose–Einstein condensation exists in the fitness model even without mapping to a Bose gas.A similar relation can be seen in models with super linear preferential attachment, however, it is not clear whether this is an accident or a deeper connection lies between this and the fitness model.

Some other interesting applications of Bose–Einstein condensation

i) Evolutionary Models:

In evolutionary models each species reproduces proportionally to its fitness. Depending on the fitness distribution, the model shows a condensation phase transition. Recently the mapping of this model to a Bose–Einstein condensation was done.

ii) Ecological Systems:

When the condensation phenomenon in an ecological system occurs, one species becomes dominant and strongly reduces the biodiversity of the system. This phase transition describes a basic stylized mechanism which is responsible for the large impact of invasive species in many ecological systems.

iii) Memory Explanation:

In 1970 Pascual-Leone had shown that memory experiments can be modelled by the Bose–Einstein occupancy model.From this and a large body of other empirical findings, Weiss and Weiss draw the generalized conclusion that memory span can be understood as the quantum number of a harmonic oscillator, where memory is to be mapped into an equilibrium Bose gas.

P.S. : May be this blog is missing Sehwagian flare, but if you can get slightest hint of class of cover drive by Ganguly, my effort will be justified :)

References

1. Bianconi, G.; Barabási, A.-L. (2001). "Bose–Einstein Condensation in Complex Networks." Phys. Rev. Lett. 86: 5632–35.

2. Albert, R.; Barabási, A.-L. (2002). "Statistical mechanics of complex networks" Rev. Mod. Phys. 74: 47–97.

3. Bose, S. N. (1924). "Plancks Gesetz und Lichtquantenhypothese". Zeitschrift für Physik 26: 178.

4. Einstein, A. (1925). "Quantentheorie des einatomigen idealen Gases". Sitzungsberichte der Preussischen Akademie der Wissenschaften

5. http://en.wikipedia.org/wiki/Bose%E2%80%93Einstein_condensate

Six Degrees - CNT 2013 at CSE, IITKgp

Friday 11 January 2013

Bose–Einstein Condensation: a Complex Network Approach

Bose–Einstein condensate:

Connection with network theory

Bose–Einstein phase transition in complex networks

Some other interesting applications of Bose–Einstein condensation

References

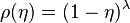
No comments:

Post a Comment

Contributors