Deep Learning Artificial Neural Networks and Restricted Boltzmann Machines

What is a Neural Network and Deep Learning in Artificial Neural Networks?

An Artificial Neural Network (ANN) is an information processing paradigm that is inspired by the way biological nervous systems, such as the brain, process information. It is composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process.

Deep learning is part of a broader family of machine learning methods based on learning representations.For example an observation can be better represented in many ways but some representations make it easier to learn tasks of interest.So research in this area works on better representations and how to learn them.

The new version of Accord.NET brings a nice addition for those working with machine learning and pattern recognition : Deep Neural Networks and Restricted Boltzmann Machines

Below is a class diagram for an instance of Deep Neural Network:

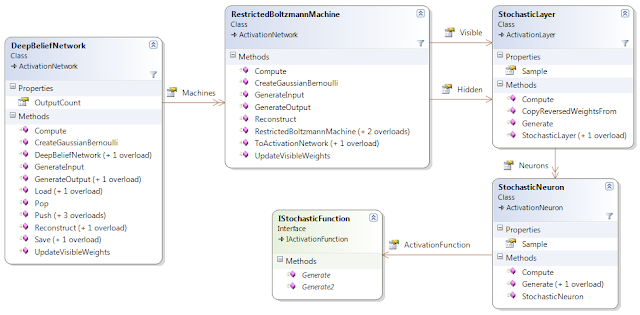Class diagram for Deep Neural Networks in the Accord.Neuro namespace

But why more layers?

The Universal Approximation Theorem (Cybenko 1989; Hornik 1991) states that a standard multi-layer activation neural network with a single hidden layer is already capable of approximating any arbitrary real function with arbitrary precision. Why then create networks with more than one layer?

To reduce complexity. Networks with a single hidden layer may arbitrarily approximate any function, but they may require an exponential number of neurons to do so. Example: Any boolean function can be expressed using only a single layer of AND, OR and NOT gates (or even only NAND gates). However, one would hardly use only this to fully design, let's say, a computer processor. Rather, specific behaviors would be modeled in logic blocks, and those blocks would then be combined to form more complex blocks until we create a all-compassing block implementing the entire CPU.

 By allowing more layers we allow the network to model more complex behavior with less activation neurons; futhermore the first layers of the network may specialize on detecting more specific structures to help in the later classification. Dimensionality reduction and feature extraction could have been performed directly inside the network on its first layers rather than using specific separate algorithms.

Do computers dream of electric sheep?

The key insight in learning deep networks was to apply a pre-training algorithm which could be used to tune individual hidden layers separately. Each layer is learned separately without supervision. This means the layers are able to learn features without knowing their corresponding output label. This is known as a pre-training algorithm because, after all layers have been learned unsupervised, a final supervised algorithm is used to fine-tune the network to perform the specific classification task at hand.

As shown in the class diagram on top of this post, Deep Networks are simply cascades of Restricted Boltzmann Machines (RBMs). Each layer of the final network is created by connecting the hidden layers of each RBM as if they were hidden layers of a single activation neural network.

Now, the most interesting part about this approach will be given now. It is about one specific detail on how the RBMs are learned, which in turn allows a very interesting use of the final networks. As each layer is a RBM learned using an unsupervised algorithm, they can be seen as standard generative models. And if they are generative, they can be used to reconstruct what they have learned. And by sequentially alternating computation and reconstruction steps initialized with a random observation vector, the networks may produce patterns which have been created using solely they inner knowledge about the concepts it has learned. This may be seen fantastically close to the concept of a dream.

Further Reading:

1. Bengio, Y. (2009). Learning Deep Architectures for AI.. Now Publishers.

2. K. Fukushima. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36(4): 93-202, 1980.

3. M Riesenhuber, T Poggio. Hierarchical models of object recognition in cortex. Nature neuroscience, 1999.

4. S. Hochreiter. Untersuchungen zu dynamischen neuronalen Netzen. Diploma thesis, Institut f. Informatik, Technische Univ. Munich, 1991. Advisor: J. Schmidhuber

5. S. Hochreiter, Y. Bengio, P. Frasconi, and J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001.

6. Hochreiter, Sepp; and Schmidhuber, Jürgen; Long Short-Term Memory, Neural Computation, 9(8):1735–1780, 1997

7. http://blogs.technet.com/b/next/archive/2012/06/20/a-breakthrough-in-speech-recognition-with-deep-neural-network-approach.aspx#.UVJuIBxHJLk