Protein-Protein
Interaction(PPI) Analysis
Introduction
Systems biology is an emerging approach applied to
biomedical and biological scientific research. Systems biology is a
biology-based inter-disciplinary field of study that focuses on complex
interactions within biological systems, using a more holistic perspective (holism instead
of the more traditional reductionism) approach to biological and biomedical research.
Networks analysis
in Systems Biology
One important toolkit of
systems biology is network analysis. Network models are useful representations
of several biological systems, ranging from metabolic pathways to ecosystems . Network analysis has its roots in
sociology where sociologists were (and still are) interested in the patterns of
interactions between people in groups. Various methodologies of network
analyzing tools were invented to describe network structures at the microscopic
and the macroscopic levels. We can simply use degree centrality or we can
employ more complicated methods by quantifying, for instance, the shortest
distance (d)
between a focal node and one other node, and then sum those distances up for
all others as a proxy to its network position (a distance here refers to the number
of links the focal node needs to traverse in order to reach the target node)
with all others in the same social network. At the level of a network, network
properties can be quantified by collecting information from the nodal level;
this ranges from simple measures like link density, which is the number of
observed links divided by the total amount possible, to more complicated one
such as the averaged shortest distance between any node pairs. Several
disciplines have borrowed the concept of network analysis from the sociologists
in the last decade.
In PPI networks, graph nodes
represent proteins, and links represent their interactions. Interactions can
often be of two types. In the simplest case, an unsigned and undirected link
exists between two proteins if they form a (part of a) protein complex
pertaining to certain cellular functions. In the other case, a directed and
signed link from one protein to another one exists if the former regulates
(positively or negatively) the latter one. The first
type of interaction is more common in PPI network studies, whereas the second
type is more adequate for modelling signal transduction networks. It is
important to note that the particular research problem and the available
database largely determine exactly which network analytical tools can be used
for analysis.
Case study
The S. cerevisiae
protein-protein interaction network which was investigate by H. Jeong, S. P.
Mason, A.-L. Barabásil and Z. N. Oltvai has 1870 proteins as nodes, connected
by 2240 identified direct physical interactions, and is derived from combined,
non-overlapping data obtained mostly by systematic two-hybrid analyses.
Their first goal was to
identify the architecture of this network, determining if it is best described by
an inherently uniform exponential topology with proteins on average possessing
the same number of links, or by a highly heterogeneous scale-free topology with
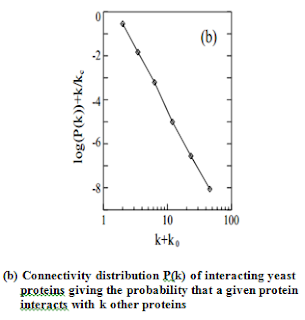
proteins having widely different connectivity . As they show in Fig. b, the probability
that a given yeast protein interacts with k other yeast proteins follows a
power-law 5 with an exponential cutoff at kc≅ 20, a topology that is also
shared by the protein-protein interaction network of the bacterium, H. pylori.
This indicates that the network of protein interactions in two separate
organisms forms a highly non-homogeneous scale-free network in which a few
highly connected proteins play a central role in mediating interactions among
numerous, less connected proteins.
An important known
consequence of the non-homogeneous structure is the network’s simultaneous
tolerance against random errors coupled with fragility against the removal of
the most connected nodes. Indeed, they found that random mutations in the
genome of S. cerevisiae, modeled by the removal of randomly selected yeast
proteins do not affect the overall topology of the network. In contrast, when the most connected proteins are computationally
eliminated, the network diameter increases rapidly.
This simulated
tolerance against random mutation is in agreement with systematic mutagenesis
studies, which identified a striking capacity of yeast to tolerate the deletion
of a substantial number of individual proteins from its proteome. Yet, if
indeed this is due to a topological component to error tolerance, on average
less connected proteins should prove less essential than highly connected ones.
To assess this
hypothesis, they rank ordered all interacting proteins based on the number of
links they have and correlated this with the phenotypic effect of their
individual removal from the yeast proteome.
As shown in Fig. c,
the likelihood that removal of a protein will prove lethal clearly correlates
with the number of interactions the protein has.
Inference
The simultaneous
emergence of an inhomogeneous structure in both metabolic and protein
interaction
networks indicates the evolutionary selection of a common large scale structure
of biological
networks, and
strongly suggests that future systematic protein-protein interaction studies in
other
organisms will
uncover an essentially identical protein network topology. The correlation
between the
connectivity and
indispensability of a given protein confirms that despite the importance of
individual
biochemical
function and genetic redundancy, the robustness against mutations in yeast is
also derived
from the
organization of interactions and topologic position of individual protein.
Thus, a better
understanding of
cell dynamics and robustness will be obtained from integrated approaches that
simultaneously
incorporate the individual and contextual properties of all constituents of
complex
cellular networks.
References
1. http://en.wikipedia.org/wiki/Systems_biology
2. Ferenc Jordian, Thanh Phuong Nguyen, Wei-Chung,Liu-Studying protein-protein interaction networks: a system view on diseases
3. H.Jeong, S.P.Mason, A.L.Barabasi and Z.L.Oltvai-Lethality ad centrality in protein networks


No comments:
Post a Comment